Aprendiendo a instalar WordPress
Un tutorial paso a paso para ayudarte a instalar WordPress. Da el primer paso para comenzar tus proyectos webs y darle vida a esa idea
Algoritmos de ordenación: Bubble sort, Counting Sort, Quick Sort y muchos mas
Los algoritmos de ordenación son esenciales en la informática moderna. Desde la organización de bases de datos hasta la optimización de procesos en inteligencia artificial, estos métodos permiten ordenar datos de manera eficiente para mejorar el rendimiento de los sistemas.
Existen diferentes métodos de ordenación, cada uno con ventajas y desventajas según el caso de uso. Entre los más conocidos se encuentran Bubble Sort, QuickSort, Merge Sort, HeapSort, Counting Sort y Radix Sort. Algunos, como Insertion Sort y Selection Sort, son fáciles de entender pero poco eficientes en grandes volúmenes de datos, mientras que otros, como QuickSort, se utilizan en aplicaciones de alto rendimiento debido a su velocidad.
En este artículo, exploraremos los algoritmos de ordenamiento más utilizados, sus características y cuándo es recomendable utilizar cada uno. Si alguna vez te has preguntado cuál es el mejor algoritmo de ordenación según la situación, aquí encontrarás una guía completa para entender sus ventajas y diferencias.
Algoritmos de ordenación: Definición, propósito y características
Tabla de contenidos
¿Qué es un algoritmo de ordenación y para qué sirve?
Un algoritmo de ordenación es un conjunto de pasos diseñados para organizar elementos en un orden específico, generalmente ascendente o descendente. Son fundamentales en el manejo de datos, ya que optimizan procesos como la búsqueda y el análisis eficiente de información.
Ejemplo práctico
Imagina que tienes una lista desordenada de números:
[8, 3, 1, 6, 5]
Si por ejemplo aplicamos un algoritmo de ordenamiento como Bubble Sort para ordenar ascendentemente nuestra lista de números nos quedaría:
[1, 3, 5, 6, 8]
Este mismo concepto se aplica a listas de nombres, fechas y otros tipos de datos en sistemas reales.
Características de los algoritmos de ordenación
Para elegir el mejor algoritmo de ordenamiento, es clave conocer sus principales características:
- Estabilidad: Un algoritmo es estable si mantiene el orden relativo de los elementos iguales. Esto es crucial en bases de datos y sistemas donde los registros tienen prioridad.
- Complejidad temporal: Se mide en O(n²), O(n log n), etc., y define el tiempo que tarda en ejecutarse según el tamaño de los datos.
- Complejidad espacial: Indica cuánta memoria adicional usa el algoritmo, especialmente si necesita estructuras extra para funcionar.
- Ordenación en su lugar (in-place) vs. no in-place:
- In-place: No requiere memoria adicional significativa (ej. QuickSort).
- No in-place: Usa estructuras adicionales (ej. Merge Sort).
Tipos de algoritmos de ordenación y su clasificación
Los algoritmos de ordenación se pueden clasificar de diversas formas según su funcionamiento y eficiencia. A continuación, exploramos sus principales categorías.
Clasificación según el método de operación
Los algoritmos de ordenación pueden dividirse en dos grupos principales según cómo procesan los datos:
Algoritmos de comparación
Utilizan comparaciones entre elementos para determinar su posición en la lista. Son los más comunes y aplicables a cualquier tipo de datos.
Ejemplos: QuickSort, Merge Sort, HeapSort, Bubble Sort.
Algoritmos no comparativos
No dependen de comparaciones, sino de propiedades específicas de los datos (como la distribución de valores). Suelen ser más eficientes en casos concretos.
Ejemplos: Counting Sort, Radix Sort, Bucket Sort.
Clasificación según la eficiencia y rendimiento
El rendimiento de los algoritmos varía según su complejidad y uso práctico.
Algoritmos de ordenación simple
Son fáciles de implementar, pero ineficientes en listas grandes debido a su alta complejidad temporal.
Ejemplos: Bubble Sort, Selection Sort, Insertion Sort.
Algoritmos de ordenación eficiente
Son utilizados en aplicaciones reales por su alto rendimiento, especialmente con grandes volúmenes de datos.
Ejemplos: QuickSort, Merge Sort, HeapSort.
Algoritmos de ordenación simple: Bubble Sort, Selection Sort e Insertion Sort
Los algoritmos de ordenación simple son fáciles de entender e implementar, pero su rendimiento no es óptimo en grandes volúmenes de datos. Aun así, son fundamentales para comprender cómo funciona la ordenación y pueden ser útiles en casos específicos.
Bubble Sort (Ordenamiento burbuja): cómo funciona y cuándo usarlo
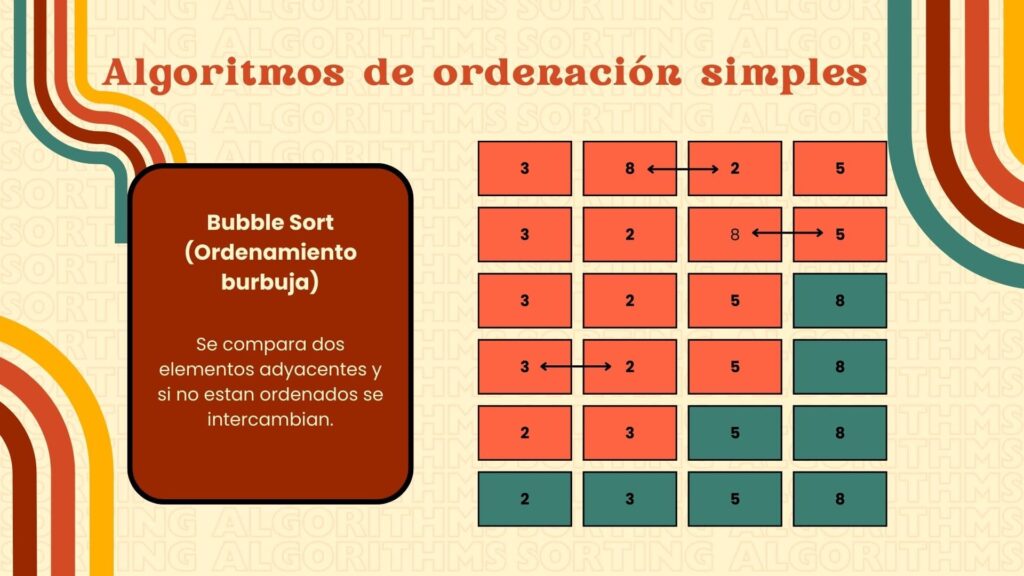
¿Cómo funciona el algoritmo Bubble Sort?
Bubble Sort recorre repetidamente la lista, comparando elementos adyacentes y intercambiándolos si están en el orden incorrecto. Este proceso hace que los elementos más grandes “floten” hacia el final de la lista en cada pasada. Se repite hasta que no se necesitan más intercambios, lo que indica que la lista está ordenada.
Análisis de complejidad de Bubble Sort
La eficiencia de Bubble Sort depende del estado inicial de la lista:
- Peor y promedio caso: O(n²)
- Mejor caso (lista ya ordenada): O(n)
Aunque es sencillo de implementar, Bubble Sort realiza muchos más intercambios que otros algoritmos como Selection Sort, por lo que no es el más eficiente para listas grandes.
Selection Sort (Ordenamiento por selección): concepto y comparación con Bubble Sort
¿Cómo funciona el algoritmo Selection Sort?
Selection Sort divide la lista en dos partes: una ordenada y otra desordenada. En cada iteración, busca el elemento más pequeño en la parte desordenada y lo intercambia con el primer elemento de esa sección. Se repite este proceso hasta que toda la lista esté ordenada.
Análisis de complejidad de Selection Sort
Selection Sort siempre realiza el mismo número de comparaciones sin importar el estado inicial de la lista:
- Peor, promedio y mejor caso: O(n²)
- Su principal ventaja es que realiza menos intercambios que Bubble Sort, lo que lo hace más eficiente en algunos escenarios.
Diferencias clave entre Selection Sort y Bubble Sort
Aunque ambos tienen la misma complejidad, Selection Sort es más eficiente en términos de intercambios, ya que solo hace uno por cada iteración (en lugar de múltiples como Bubble Sort). Sin embargo, Bubble Sort puede detenerse antes si la lista ya está ordenada, lo que le da una ventaja en listas casi ordenadas.
Insertion Sort (Ordenamiento por inserción): ventajas y casos de uso
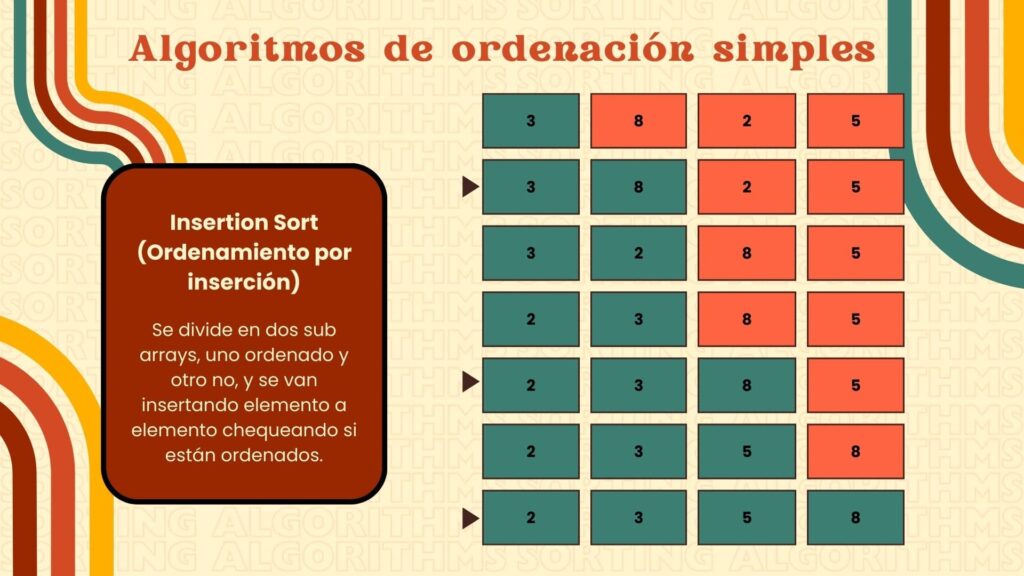
¿Qué es Insertion Sort y cómo funciona?
Insertion Sort construye la lista ordenada elemento por elemento. En cada iteración, toma un elemento de la parte desordenada y lo inserta en la posición correcta dentro de la parte ordenada. Su comportamiento es similar a cómo una persona ordenaría un mazo de cartas en la mano.
Complejidad temporal de Insertion Sort
Insertion Sort tiene un rendimiento variable según el estado inicial de la lista:
- Peor caso: O(n²) (cuando la lista está en orden inverso).
- Mejor caso: O(n) (cuando la lista ya está casi ordenada, ya que solo necesita pocos movimientos).
¿Cuándo Insertion Sort es mejor que Bubble Sort y Selection Sort?
Insertion Sort es más eficiente en listas pequeñas y casi ordenadas, ya que su mejor caso es O(n), lo que lo hace más rápido que los otros dos en estos escenarios. Además, tiene menos intercambios que Bubble Sort y suele ser más eficiente que Selection Sort en listas parcialmente ordenadas.
Algoritmos de ordenación eficientes
Estos algoritmos son ampliamente utilizados en aplicaciones reales gracias a su rendimiento confiable, especialmente cuando se trabaja con grandes volúmenes de datos.
Merge Sort (Ordenamiento por mezcla)
Explicación del algoritmo y su enfoque divide y vencerás
Merge Sort sigue el paradigma de divide y vencerás. Divide recursivamente la lista en mitades hasta que cada sublista tenga un solo elemento, y luego las vuelve a unir de forma ordenada. Esta estrategia permite ordenar eficientemente sin necesidad de comparar cada elemento con todos los demás.
Análisis de complejidad: O(n log n) en todos los casos
- Mejor, peor y promedio caso: O(n log n)
- Utiliza espacio adicional para realizar las fusiones.
Ventajas y desventajas respecto a QuickSort
Ventajas:
- Rendimiento constante sin importar el orden inicial de los datos.
- Es estable (mantiene el orden relativo de elementos iguales).
- Ideal para listas enlazadas o estructuras no contiguas.
Desventajas:
- Requiere más memoria por el uso de arreglos auxiliares.
- Puede ser más lento que QuickSort en listas pequeñas o con buena distribución.
QuickSort (Ordenamiento rápido)
Explicación del algoritmo y la elección del pivote
QuickSort también usa divide y vencerás, pero con un enfoque diferente. Elige un pivote y reorganiza la lista para que todos los elementos menores queden a la izquierda y los mayores a la derecha. Luego repite el proceso recursivamente.
La elección del pivote afecta directamente su rendimiento. Si se elige mal (por ejemplo, siempre el menor o mayor), el algoritmo puede volverse ineficiente.
Análisis de complejidad: O(n log n) en el mejor caso, O(n²) en el peor
- Mejor y promedio caso: O(n log n)
- Peor caso: O(n²), aunque es poco común con pivote aleatorio o técnicas de optimización.
Comparación con Merge Sort:
| Criterio | Merge Sort | QuickSort |
|---|---|---|
| Complejidad (peor caso) | O(n log n) | O(n²) |
| Uso de memoria | Mayor (no in-place) | Menor (in-place) |
| Estabilidad | Estable | No estable |
| Rendimiento en la práctica | Consistente | Muy rápido |
HeapSort (Ordenamiento por montículos)
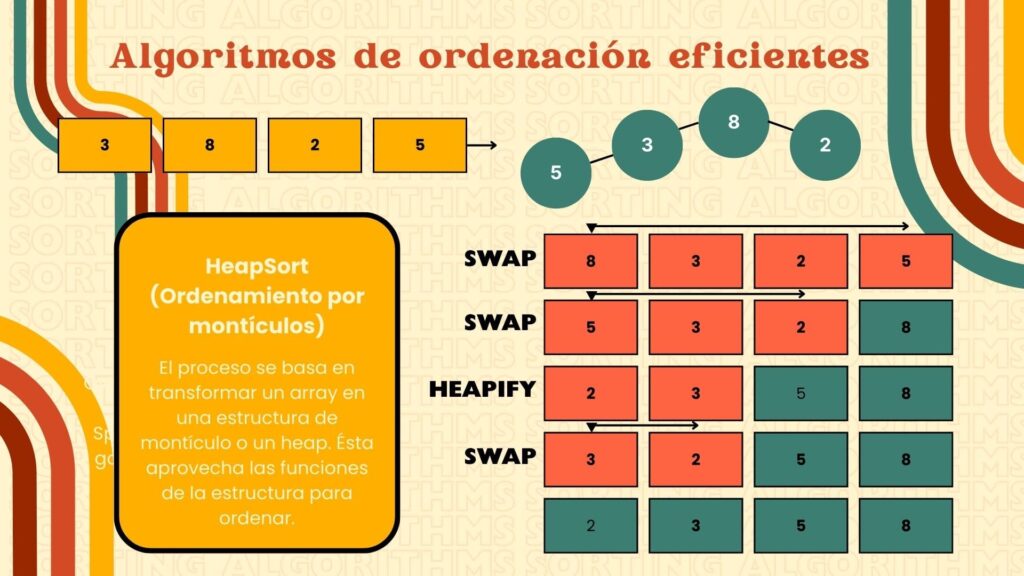
Explicación del algoritmo y uso de un heap
HeapSort se basa en una estructura llamada heap binario, que permite acceder rápidamente al mayor (o menor) elemento. El algoritmo transforma el arreglo en un heap y luego extrae el valor máximo repetidamente, reordenando el heap en cada paso hasta dejar la lista ordenada.
Análisis de complejidad: O(n log n)
- Mejor, peor y promedio caso: O(n log n)
- Funciona completamente in-place, sin uso adicional de memoria.
Cuándo usar HeapSort en lugar de QuickSort o MergeSort
- Cuando se necesita consumo de memoria constante.
- Cuando se requiere rendimiento predecible y consistente, sin sorpresas en el peor caso.
- Útil en sistemas donde no se permite el uso de memoria extra, como en dispositivos embebidos o sistemas de tiempo real.
Algoritmos de ordenación no comparativos: Counting Sort y Radix Sort
Los algoritmos de ordenación no comparativos forman una categoría especial que no se basa en comparar elementos entre sí. En lugar de eso, utilizan características internas de los datos, como sus dígitos o valores exactos. Son extremadamente eficientes cuando se aplican en los contextos adecuados, superando incluso a los algoritmos comparativos más conocidos en términos de velocidad.
Counting Sort (Ordenamiento por conteo): cómo funciona y cuándo aplicarlo
¿Cómo funciona Counting Sort?
Counting Sort ordena elementos contando cuántas veces aparece cada valor dentro de un rango específico. A partir de ese conteo, reconstruye la lista en orden.
Ejemplo práctico:
Si tenemos una lista con valores entre 0 y 9, el algoritmo crea un arreglo auxiliar para registrar cuántas veces aparece cada número. Luego, usa esa información para ubicar los elementos en sus posiciones correctas.
Complejidad de Counting Sort: O(n + k)
- La n representa la cantidad de elementos a ordenar.
- La k representa el rango de valores posibles.
Esto significa que es muy rápido cuando el rango (k) es pequeño en relación con la cantidad de datos (n).
¿Cuándo usar Counting Sort y cuáles son sus límites?
Ventajas:
- Ordenación extremadamente rápida para enteros pequeños y positivos.
- Ideal cuando los valores no varían demasiado.
- No usa comparaciones, lo que le da una ventaja sobre algoritmos como QuickSort en ciertos casos.
Limitaciones:
- No sirve para datos con un rango muy amplio (por ejemplo, edades entre 1 y 10,000).
- No puede aplicarse directamente a números con decimales, valores negativos o estructuras más complejas como strings (a menos que se adapten).
Radix Sort (Ordenamiento por base): una alternativa eficiente
¿Cómo funciona Radix Sort?
Radix Sort trabaja sobre los dígitos individuales de los números, desde el dígito menos significativo hasta el más significativo (o al revés). Es ideal para ordenar números enteros de varios dígitos.
🔍 Ejemplo práctico:
Para una lista de números entre 100 y 999, Radix Sort puede ordenar primero por la unidad, luego por la decena y finalmente por la centena. Esto se repite hasta que todos los dígitos han sido procesados.
Complejidad de Radix Sort: O(nk)
- n: cantidad de elementos a ordenar.
- k: número de dígitos del número más grande.
Es lineal si k es pequeño, lo que suele ser cierto en muchas aplicaciones prácticas.
Comparación entre Radix Sort y Counting Sort
| Criterio | Radix Sort | Counting Sort |
|---|---|---|
| Tipo de dato | Números enteros con varios dígitos | Enteros simples en un rango limitado |
| Rango de valores | Funciona aunque el rango sea amplio | Necesita un rango acotado y pequeño |
| Velocidad | Alta, si k (dígitos) es pequeño | Muy alta, si k (valores únicos) es bajo |
| Espacio en memoria | Puede requerir más espacio auxiliar | También usa espacio extra, pero menos |
| Aplicaciones típicas | Ordenar identificadores, claves, etc. | Edad de personas, calificaciones, etc. |
Comparación entre los algoritmos de ordenación
Elegir el algoritmo de ordenación adecuado puede marcar una gran diferencia en el rendimiento, especialmente cuando se trata de trabajar con grandes volúmenes de datos. A continuación, analizamos y comparamos los algoritmos más populares en base a su complejidad y casos de uso.
Comparación de complejidades: O(n²), O(n log n) y O(n + k)
| Algoritmo | Mejor caso | Promedio | Peor caso | Uso recomendado |
|---|---|---|---|---|
| Bubble Sort | O(n) | O(n²) | O(n²) | Listas pequeñas y casi ordenadas |
| Selection Sort | O(n²) | O(n²) | O(n²) | Pequeñas listas sin restricciones de rendimiento |
| Insertion Sort | O(n) | O(n²) | O(n²) | Listas pequeñas y casi ordenadas |
| Merge Sort | O(n log n) | O(n log n) | O(n log n) | Grandes listas, ordenación estable |
| QuickSort | O(n log n) | O(n log n) | O(n²) | Ordenación rápida en la mayoría de los casos |
| HeapSort | O(n log n) | O(n log n) | O(n log n) | Cuando se necesita ordenación sin memoria extra |
| Counting Sort | O(n + k) | O(n + k) | O(n + k) | Datos con rango pequeño y conocido |
| Radix Sort | O(nk) | O(nk) | O(nk) | Datos numéricos con pocos dígitos |
¿Cuál es el mejor algoritmo de ordenación para cada situación?
¿Estás ordenando listas pequeñas o grandes?
- Para listas pequeñas (por ejemplo, menos de 100 elementos), los algoritmos sencillos como Insertion Sort o Bubble Sort pueden ser suficientes, especialmente si los datos ya están parcialmente ordenados.
- Para listas grandes, es preferible usar algoritmos más eficientes como Merge Sort, QuickSort o HeapSort, todos con complejidad O(n log n).
¿Tus datos están casi ordenados o completamente desordenados?
- Si los datos están casi ordenados, Insertion Sort es una excelente opción debido a su mejor caso O(n).
- Para datos completamente aleatorios, QuickSort suele ser el más rápido en la práctica, aunque Merge Sort ofrece un rendimiento más predecible y estable.
¿Disponés de memoria limitada o podés usar memoria extra?
- En sistemas con restricciones de memoria, HeapSort es ideal ya que no requiere espacio adicional.
- En cambio, Merge Sort, aunque muy eficiente, necesita memoria extra para su proceso de mezcla, lo cual puede ser una desventaja en entornos limitados.
¿Estás trabajando con números enteros en rangos específicos?
- Si los datos son números enteros dentro de un rango conocido y pequeño, Counting Sort es extremadamente eficiente.
- Para números más grandes pero con pocos dígitos, Radix Sort puede superar a QuickSort en rendimiento.
Optimización y variantes de los algoritmos de ordenación
Los algoritmos de ordenación no son estáticos: con el tiempo, se han desarrollado optimizaciones inteligentes y variantes híbridas para mejorar su rendimiento según el tipo de datos y el entorno de ejecución.
Mejoras en los algoritmos básicos
Optimización de Bubble Sort: detección de listas ya ordenadas
Bubble Sort puede mejorarse usando una bandera (flag) que verifique si se realizaron intercambios durante una pasada. Si no se hicieron cambios, significa que la lista ya está ordenada y el algoritmo puede detenerse anticipadamente.
Esto reduce la complejidad en el mejor caso a O(n), en lugar de hacer todas las pasadas innecesarias.
Insertion Sort con búsqueda binaria
Insertion Sort suele buscar la posición de inserción en O(n). Pero si se reemplaza esa búsqueda lineal por una búsqueda binaria, se reduce ese tiempo a O(log n).
Aun así, la complejidad total sigue siendo O(n²) por los desplazamientos de elementos, pero gana eficiencia en listas parcialmente ordenadas.
Variantes híbridas de algoritmos
Los algoritmos híbridos combinan las fortalezas de varios métodos para adaptarse mejor a distintas situaciones.
Introsort: lo mejor de QuickSort y HeapSort
Introsort (Introduced Sorting) comienza usando QuickSort por su rapidez promedio, pero si detecta que la recursión se está profundizando demasiado (lo que indica un caso desfavorable), cambia automáticamente a HeapSort, garantizando una complejidad O(n log n) incluso en el peor caso.
Este enfoque lo hace altamente robusto y confiable, y por eso es el algoritmo por defecto en la STL (Standard Template Library) de C++.
Timsort: el algoritmo inteligente detrás de Python y Java
Timsort es un algoritmo híbrido que combina Insertion Sort y Merge Sort.
- Detecta “runs” (segmentos ya ordenados en la lista).
- Usa Insertion Sort para ordenar esos segmentos si son pequeños.
- Luego los combina usando Merge Sort.
Este enfoque hace que Timsort sea increíblemente eficiente para listas parcialmente ordenadas, que son comunes en aplicaciones reales.
Por eso es el algoritmo de ordenación predeterminado en Python y Java.
Aplicaciones de los algoritmos de ordenación en el mundo real
Los algoritmos de ordenación no solo son importantes en teoría: tienen un rol crucial en el rendimiento de sistemas reales, desde bases de datos hasta inteligencia artificial.
Ordenación en bases de datos y sistemas de búsqueda
Los sistemas de bases de datos utilizan ordenación para mejorar la eficiencia de consultas y operaciones complejas:
- Índices ordenados (como B-Trees) permiten realizar búsquedas binarias rápidas, minimizando el tiempo de respuesta en bases de datos relacionales.
- Operaciones de JOIN optimizadas: cuando las tablas están ordenadas, las uniones pueden ejecutarse con algoritmos de fusión más eficientes (merge join), reduciendo el coste computacional.
Ordenación en inteligencia artificial y machine learning
En el campo del aprendizaje automático, ordenar datos es una etapa crítica del preprocesamiento:
- Limpieza de datos: ordenar valores categóricos o eliminar duplicados antes de alimentar modelos mejora la calidad de entrenamiento.
- Algoritmos de clustering como k-means se benefician de datos ordenados para reducir iteraciones y acelerar convergencia.
Aplicaciones en redes y procesamiento de imágenes
La ordenación también es esencial en disciplinas como las telecomunicaciones y la visión por computadora:
- Protocolos de red como TCP reordenan los paquetes de datos que llegan desorganizados, garantizando su entrega en el orden correcto.
- Filtros de mediana en imágenes ordenan los valores de píxeles dentro de pequeñas ventanas para eliminar ruido sin afectar los bordes, lo cual es útil en tareas como reconocimiento facial o análisis de imágenes médicas.
Conclusión: Dominando los Algoritmos de Ordenación y su Aplicación Práctica
Resumen de los puntos clave
A lo largo de este artículo, hemos explorado los algoritmos de ordenación más comunes y sus aplicaciones en diferentes escenarios. Estos algoritmos son esenciales para mejorar el rendimiento en diversas áreas, desde el procesamiento de grandes volúmenes de datos hasta la optimización de sistemas en inteligencia artificial, bases de datos y redes.
- Algoritmos básicos: Hemos cubierto algoritmos como Bubble Sort, Selection Sort, Insertion Sort, que son fáciles de entender pero no son eficientes para grandes conjuntos de datos.
- Algoritmos eficientes: Algoritmos como Merge Sort, QuickSort y HeapSort son mucho más adecuados para trabajar con listas grandes gracias a su complejidad O(n log n).
- Algoritmos no comparativos: Counting Sort y Radix Sort se destacaron por su capacidad de ordenar en tiempo O(n + k) y O(nk), siendo ideales para escenarios específicos como datos numéricos con rangos pequeños.
- Mejoras y variantes híbridas: La evolución de algoritmos básicos con optimizaciones como Introsort y Timsort mejoran significativamente su rendimiento en diferentes contextos.
- Aplicaciones prácticas: Los algoritmos de ordenación no solo se utilizan en teoría, sino que juegan un papel clave en la optimización de sistemas de bases de datos, machine learning, procesamiento de imágenes y redes.
Recomendaciones sobre qué algoritmos aprender primero
Si estás comenzando en el mundo de los algoritmos de ordenación, te recomiendo seguir este orden de aprendizaje para obtener una base sólida y luego avanzar a temas más complejos:
- Comienza con algoritmos básicos: Asegúrate de entender los principios fundamentales de Bubble Sort, Selection Sort y Insertion Sort. Aunque no son eficientes para grandes conjuntos de datos, te ayudarán a comprender cómo funcionan los algoritmos de ordenación y los conceptos como comparación de elementos y intercambio.
- Pasa a algoritmos más eficientes: Una vez que te sientas cómodo con los básicos, estudia Merge Sort y QuickSort. Estos algoritmos te permitirán comprender la técnica de divide y vencerás y cómo optimizar el rendimiento para listas grandes.
- Aprende algoritmos no comparativos: Después de dominar los algoritmos comparativos, explora Counting Sort y Radix Sort. Estos algoritmos no dependen de comparaciones directas entre elementos, por lo que ofrecen soluciones más rápidas en situaciones específicas.
- Estudia variantes híbridas: Finalmente, profundiza en algoritmos híbridos como Timsort e Introsort, que combinan técnicas de varios algoritmos para mejorar el rendimiento en casos prácticos.
Enlaces a recursos adicionales para seguir profundizando
Para seguir aprendiendo sobre algoritmos de ordenación y otros temas de algoritmos y estructuras de datos, aquí tienes algunos recursos recomendados:
- GeeksforGeeks: Una plataforma increíblemente completa con ejemplos, explicaciones detalladas y problemas prácticos sobre algoritmos y estructuras de datos.
- Coursera – Algoritmos de Stanford: Un curso excelente de Stanford sobre algoritmos que cubre desde lo más básico hasta algoritmos más complejos y aplicaciones avanzadas.
- VisuAlgo: Una herramienta interactiva para visualizar cómo funcionan los algoritmos de ordenación y otros algoritmos comunes, lo que facilita su comprensión.
- Estructuras de datos y algoritmos en Python (Libro): Un libro excelente para profundizar en la implementación de algoritmos en Python.
- LeetCode: Un sitio web ideal para practicar algoritmos de ordenación y otros problemas de algoritmos en escenarios de la vida real.
Próximos pasos en tu aprendizaje
Recuerda que el aprendizaje de algoritmos de ordenación es solo el principio. Estos principios fundamentales de ordenación te proporcionarán las bases para abordar problemas más complejos, como algoritmos de búsqueda, algoritmos de grafos, programación dinámica y más.
Si estás desarrollando un software o trabajando en proyectos de inteligencia artificial, bases de datos o redes, estos algoritmos son herramientas esenciales para mejorar el rendimiento y eficiencia de tus sistemas.
¡Sigue explorando y practicando, y verás cómo tu comprensión de los algoritmos de ordenación te ayudará a resolver problemas más complejos con mayor eficacia!
Explora nuestros artículos relacionados
Introducción a las estructuras de datos
Las estructuras de datos son una pieza fundamental en la programación, no importa en el nivel que estés. Es importante conocer las estructuras mas importantes y sacarle el máximo provecho a ellas!
¿Cómo mejorar el CTR de tu página web?
El CTR es una de las métricas mas importantes, es el porcentaje de personas que ingresan a tu página. Averigua como aumentar esta métrica tan esencial
Preguntas frecuentes
¿Qué es un algoritmo de ordenación y para qué sirve?
Un algoritmo de ordenación es un conjunto de instrucciones diseñado para organizar los elementos de una lista o arreglo en un orden específico, como ascendente o descendente. Se utilizan para mejorar la eficiencia en la búsqueda de datos, análisis, visualización y optimización de recursos en muchos programas y sistemas.
¿Cuál es el algoritmo de ordenación más fácil de entender para principiantes?
El ordenamiento burbuja (Bubble Sort) suele ser el más recomendado para principiantes por su simplicidad. Compara elementos adyacentes y los intercambia si están en el orden incorrecto, repitiendo este proceso hasta que la lista esté ordenada. Aunque no es el más eficiente, ayuda a comprender conceptos básicos como comparaciones e intercambios.
¿Qué diferencia hay entre algoritmos de ordenación estables e inestables?
Un algoritmo estable mantiene el orden original de los elementos con valores iguales, mientras que uno inestable puede cambiar ese orden. Por ejemplo, si dos productos tienen el mismo precio y se ordenan por precio, un algoritmo estable los dejará en el mismo orden en que estaban originalmente.
¿Cuál es el algoritmo más rápido en la práctica?
QuickSort suele ser uno de los algoritmos más rápidos en la práctica debido a su enfoque “divide y vencerás”, especialmente con grandes volúmenes de datos. Sin embargo, su rendimiento puede verse afectado si los datos están muy desordenados o ya casi ordenados, en cuyo caso Merge Sort puede ser más predecible y seguro.
¿Qué factores se deben considerar al elegir un algoritmo de ordenación?
Se deben considerar varios factores como:
Tamaño de los datos.
Si los datos ya están parcialmente ordenados.
Uso de memoria (in-place o no).
Necesidad de estabilidad.
Velocidad en el peor, mejor y promedio de los casos.
Cada algoritmo tiene fortalezas y debilidades según el contexto.
“Per aspera ad astra.”
A través de las dificultades hasta las estrellas.
© 2025 DevWebers. All Rights Reserved.